Jedem Mathematiker ist der Satz des Pythagoras a² + b² = c² bekannt. Über was hat er wohl nachgedacht? Stellt sich doch die Frage ob a² + b² nicht noch weitere Erkenntnisse verbirgt.
Die Antwort lautet: Ja, man kann damit das Verhältnis zwischen einem Kreisumfang und seinem Durchmesser, also π als Gerade in der Zeichnung darstellen, wenn auch nur mit einer Genauigkeit von 99,9 Prozent.
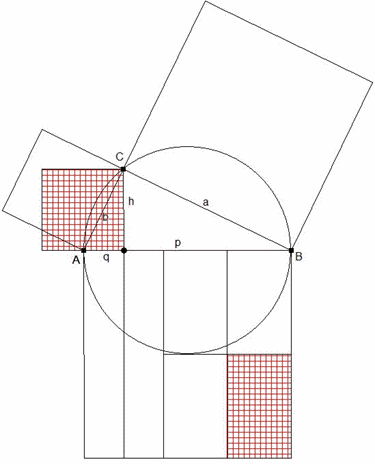
Bei der Ausarbeitung von Hans- Werner Meixner und Christian Meixner handelt es sich um die erste geometrische Ermittlung der Kreiszahl π mit Hilfe eines rechtwinkligen Dreiecks und den bekanntesten Lehrsätzen hierzu. Weitere Details findet der geneigte Leser im dazugehörigen Dokument Geometrisches-Pi [PDF / 700 KB].
Als Ergebnis schließt diese Ausarbeitung mit folgender Näherungsformel für die Kreiszahl π – geometrisch ermittelt als Gerade im Thaleskreis
Mit p + q = 4 und p – q = p * q
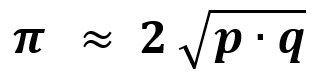
Eine Anmerkung muss ich unbedingt loss werden:
Von einem Römer wurde Archimedes von Syrakus erschlagen, als die Römer Syrakus erobert haben. Nicht Pythagoras und auch nicht Thales.
Danke, habe den Lapsus behoben und die Textpassage entfernt.