Die Mathematiker sind sich ziemlich einig, wenn es um die Frage nach der schönsten und elegantesten Gleichung bzw. Formel der Mathematik geht. Ihre Antwort lautet fast immer:
ei*pi = -1
In der Regel bevorzugen die Mathematiker eine leicht abgewandelte Form der Gleichung, so wie auf dem folgenden Foto von der Mathematica Ausstellung 2010 im Technischen Museum in Berlin zu sehen. Die Gleichung ist so beliebt, dass sie auf T-Shirts und Poster gedruckt wird 😉
In dieser Form entfaltet die Formel ihre volle Eleganz. Die Gleichung verbindet die wichtigsten Zahlen und Operatoren der Mathematik miteinander.
1 + ei*pi = 0
Das neutrale Element der Addition 0, das neutrale Element der Multiplikation 1, die Eulersche Zahl e, die imaginäre Einheit i und meine irrationale transzendente Lieblingszahl Pi werden mit Hilfe von Addition, Multiplikation und Exponentialfunktion zueinander in Relation gebracht.
Bei obiger Gleichung handelt es sich um einen Spezialfall der Eulerschen Formel bzw. Eulerschen Identität:
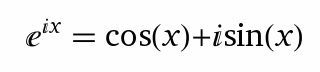
Entdeckt und veröffentlicht hat die Formel der berühmte Schweizer Mathematiker Leonhard Euler im Jahre 1748. Die Eulersche Formel / Identität lässt sich sehr anschaulich mit Hilfe von Taylor-Reihen erklären und beweisen.
Setzt man x=π in die Eulersche Formel ein, so bleibt wegen cos(π)=-1 und sin(π)=0 genau das gewünschte Resultat übrig. Das ist ein verblüffend einfaches Ergebnis für einen derart abstrakten Input 😉
Es gibt noch einige andere interessante Ansätze, um die magische Eulersche Formel e hoch (i*pi) den Menschen begreiflich zu machen. Der Mathologer versucht es z.B. mit grenzwertigen Zinseszins Berechnungen und Drehstreckungen in der Komplexen Ebene.
Wir können auch noch einen kurzen Blick auf die Zahl e hoch pi werfen. Sieht in dieser Form einfacher aus als die Formel e hoch i pi. Liefert aber ein viel krummeres Ergebnis: eπ = 23.1406926327792690… . Wenn wir diese krumme Zahl jetzt aber noch mit i potenzieren
so sind wir wieder bei unserer Eulerschen Identität Wunderzahl. Ihr könnt das Ergebnis auch mit Hilfe von Google prüfen: (e hoch pi) hoch i.
Wer bei entsprechenden Recherchen gut aufpasst, der wird erkennen, dass relativ häufig die Gleichung ei*pi = -1 auch als Eulersche Identität bezeichnet wird. Was m.E. nicht ganz korrekt ist, aber irgendwie auch gut passt 😉

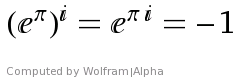
Soweit so gut, aber wenn ich beide Seiten quadriere, bekomme ich exp(2*pi*i)=1 mit 2*pi*i=0 !?
Auch wenn komplexe Nullstellen der e-Funktion den gleichen reellen Wert liefern, darf man sie nicht gleichsetzen (sh Einheitswurzeln).
e hoch 0 ist 1 für reelle Zahlen.
e hoch iz = cos z +i sin z.
Für z=2 pi kommt 1 + i×0=1 heraus.
Und wer erklärt den Käpt’n sparro nun als Freiberufler freibeuter und nimmt den pi raten zurück an alle Seefahrer auch wenn sie aus dem Allgäu kommen und die Weltmeere kennen. Im Surfmuseeum kann man es erklären
Fehmarn
2*π*i (oder in der unter Elektrotechnikern bevorzugten Konvention 2*π*j mit j statt i) ist keine Zahl, sondern ein Winkel.
|Betrag Z| * e ^ (j phi) ist die eulersche Darstellung einer komplexen Zahl Z mit dem Betrag |Z| und dem Winkel phi. phi wird häufig in Radiant statt Grad angegeben. Der Winkel phi = π bedeutet dann 180°. Die komplexe Zahl 1*e ^ (jπ) oder einfach e ^ (jπ) ist die komplexe Zahl mit Betrag 1 und dem Winkel 180° in der gaussschen Zahlenebene.
In der Komponentendarstellung wäre es die Zahl mit Realteil -1 und Imaginärteil 0, also : Z = (-1 + j0).
Wenn der Imaginärteil einer komplexen Zahl Null ist, kann die Zahl reell betrachtet werden.
Hier also schlicht Z = -1.
Das Quadrieren liefert dann einfach -1 ^ 2 = 1.
Das Gleiche passiert, wenn Du komplex bleibst.
Wie Du korrekt erkennst, gilt (e ^ (jπ)) ^ 2 = e ^ (j2π).
Dies ist die komplexe Zahl mit Betrag 1 und dem Winkel 360° (oder 2π Radiant) in der gaussschen Zahlenebene, also Z = (1 + j0). Dies ist die reelle Zahl 1.
(Wenn der Winkel in Radiant ein k-faches von π ist
(k ganze Zahl), ist der Imaginärteil der komplexen Zahl Null, die Zahl also reell.
Wenn der Winkel ein k-faches von 2π ist, ist sie zudem positiv.)
Ich verstehe von sowas nicht allzuviel (in Mathe 4-5 gehabt), aber halte das für Scharlatanerie. Könnte man nicht ebenso gut sagen, die Potenzierung mit i liefert für positive Zahlen -1 und für negative +1 ?
Also Z.B. 6*6 hoch 6*i gleich -1 sei dann die Zahl des Teufels, was unglaublich beeindruckend und elegant sei ?
(meine mail geht nicht)
Wenn man quadratische Gleichungen lösen möchte (0 = x²+px+q), so gibt es Fälle ohne Lösung für reelle Zahlen x1 und x2, so dass „0 = (x-x1) * (x-x2)“ gilt.
Durch die Einführung „komplexer“ Zahlen (z = x+iy) werden die Gleichungen 0 = z²+pz+q immer lösbar (z1 und z2): „0 = (z-z1) * (z-z2)“.
„x“ ist der (vertraute) reelle Teil von „z“.
„y“ ist auch reell, wird aber mit „i“ multipliziert.
„y“ nennt man „imaginären“ Teil einer komplexen Zahl.
„i“ ist formal die Quadratwurzel aus „-1“, in der Welt reeler Zahlen ein unsinniger Wert.
Sie heißt „imaginäre“ Einheit.
Wenn man die komplexen Zahlen sich als Ebene (auf dem Papier) vorstellt:
„x“ – der reele Teil – bildet die x-Achse
„y“ – der imaginäre Teil – bildet die y-Achse,
so kann man den Ausdruck „exp (i*phi)“ als rotierenden Vektor der Länge „1“ in der komplexen Ebene ansehen.
„phi“ ist dabei der Rotationswinkel gegen die reelle Achse x.
Es gilt dann: exp (i*phi) = cos (phi) + i * sin (phi).
„cos(phI)“ ist die Projektion des Vektors auf die „reelle“ x-Achse.
„sin(phi)“ ist die Projektion des Vektors auf die „imaginäre“ y-Achse.
Der Winkel „phi“ ist dabei im Winkelmaß zu sehen.
Eine komplette Umdrehung (man kommt also wieder dort an, wo man losgedreht hat) wäre also der Winkel „phi = 2*pi“ (also 360 Grad).
Nimmt man „phi = pi“ (also 180 Grad), so erhält man die genannte Formel:
exp (i*pi) = cos (pi) + i * sin (pi) = cos (180 Grad) + i * sin (180 Grad) = -1 + i * 0 = -1
Mit dem „Kniff“ des Rotationsgedankens (von Vektoren) als komplexe Zahlen werden viele technische und physikalische Zusammenhänge beträchlich einfacher zu verstehen. (So lässt sich die gesamte relativistische Elektrodynamik auf eine einzige (!!) Formel reduzieren („Nabla-phi = 0“)).
Die Erkenntnis, „dass man sich einmal um sich selbst drehen kann“ und wieder am Anfang landet führt zur Verallgemeinerung sogenannter „Residuen“, die erheblichen Erkenntnisgewinn in theoretischen Teilchenphysik geliefert haben (z.B. der „Spin“).