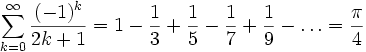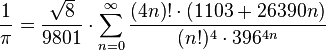Zu den ältesten Problemen in der Mathematik gehören die Berechnungen am Kreis. Sei es der Kreisumfang oder der Flächeninhalt, schon seit Tausenden von Jahren versuchen Menschen dem Kreis und seiner wundersamen Kreiskonstante die Geheimnisse zu entlocken. Waren es am Anfang nur grobe Näherungen für Pi, hat sich das mit dem Verfahren von Archimedes deutlich gewandelt. Endlich gab es eine Technik zum Berechnen der Kreiszahl Pi, die es erlaubte den Zahlenwert von π mit höherer Genauigkeit anzugeben.
Wie berechnet man Pi?
Aufgrund seiner Transzendenz und Irrationalität weiß man seit langem, dass π nicht nur eine unendlich lange Zahlenfolge darstellt, sondern dass es auch keine einfache Formel für Pi geben kann, die nur aus dem Radius oder dem Durchmesser und ein paar Divisionen und Multiplikationen den Wert von PI berechnet. Auf der anderen Seite hat man Formeln und Algorithmen entdeckt, die von verblüffender Einfachheit und Eleganz sind. Doch alle diese Formeln haben eines gemeinsam. Ohne schwere Rechenarbeit gibt es keinen Lohn. Zum Glück nehmen uns seit Mitte des Zwanzigsten Jahrhunderts moderne Rechenknechte diese Aufgabe ab. Doch angefangen hat es schon vor über 2000 Jahren mit Archimedes von Syracus.
Archimedes Verfahren / Exhaustionsmethode
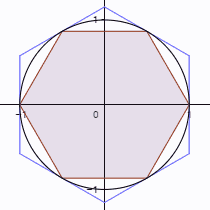Archimedes wählte für seine Berechnung von Pi einen geometrischen Ansatz. Angefangen mit zwei regelmäßigen Sechsecken, die einem Einheitskreis (Kreis mit dem Radius 1) umschrieben bzw. einbeschrieben waren, hangelte er sich über 12-, 24- und 48-Ecke bis hin zu zwei 96-Ecken. Deren Umfang berechnete er mit Hilfe der anderen Zwischenergebnisse und fand so am Ende eine untere und eine obere Grenze für deren Kreisumfang und damit auch für die Zahl Pi. Mit Hilfe der Fläche des Kreises wäre Archimedes zu ähnlichen Ergebnissen gekommen, mit wahrscheinlich etwas schwächeren Schranken.
Damit war Pi auf 2 Nachkommastellen genau berechnet und 3,14 für Jahrhunderte als erster Näherungswert von Pi etabliert. Eine starke Leistung, denn mehr als der Satz des Pythagoras und den Satz des Thales und ein paar ganz elementare geometrische Regeln standen Archimedes nicht zu Verfügung.
Pi mit unendlichen Zahlenreihen berechnen
Die vielleicht schönste und verblüffendste Formel für die Berechnung von Pi dürfte die so genannte Leibniz-Reihe sein. Sie wird Gottfried Wilhelm Leibniz zugeschrieben, soll aber schon viel früher in Indien benutzt worden sein.
Die Reihe stellt einen Sonderfall der Arcustangens Reihe dar (π/4=arctan 1). Als Rechenformel ist sie aber auf Grund ihrer schlechten Konvergenz denkbar ungeeignet. Mathematiker schufen im Laufe der Zeit viele besser geeignete Abwandlungen der Arcustangens Reihe, mit deren Hilfe Pi auf Abermillionen von Stellen berechnet werden konnte.
Mit obiger Formel berechnete ihr Entdecker John Machin 1706 immerhin 100 Stellen von Pi in Handarbeit.
Eine der frühen indischen Pi-Formeln seht ihr im Folgenden:
Die Formel geht auf den indischen Mathematiker und Astronomen Kelallur Nilakantha Somayaji (1444-1544) zurück und konvergiert nicht sonderlich schnell, witzigerweise berechnen die aufsummierten Brüche aber genau die Nachkommstellen von Pi, die 3 läuft gewissermaßen vorne weg 😉
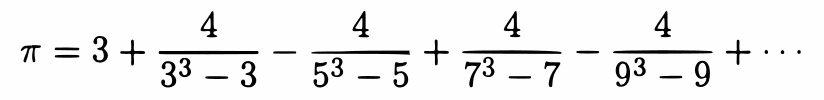
Die folgenden beiden Formeln gehen auf den großen Mathematiker Leonhard Euler zurück. Obwohl etwas komplizierter aufgrund des notwendigen Ziehens einer Wurzel, sind die doch von einer besonderen Eleganz.
Eine deutlich kompliziertere, aber sehr viel schneller konvergierende und daher auch für Berechnunge von Pi viel besser geeignete Reihenentwicklung stammte vom indischen Mathe-Genie S. Ramanujan.
