Bevor man mit Kreisflächen arbeitet, sollte man sich erst einmal überlegen, was unter einer Kreisfläche zu verstehen ist:
Unter einer Kreisfläche versteht man die Menge aller Punkte einer Ebene, die innerhalb eines Kreises (bzw. seiner Kreislinie) liegt. Man nennt die Kreisfläche „abgeschlossen“, wenn die Kreislinie zur Fläche dazu gehört, andernfalls bezeichnet man sie als „offen“.
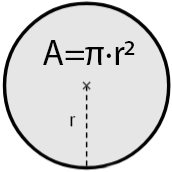Neben dem Kreisumfang ist auch der Flächeninhalt vom Kreis sehr eng mit der Kreiszahl Pi verbunden. Ist der Radius r gegeben, dann kann man mit der Formel
A = π * r2
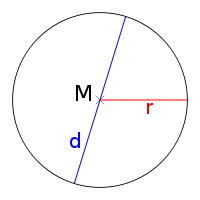
Einfacher geht nicht. Verwendet man statt des Radius den Durchmesser des Kreises, dann wäre wegen des Zusammenhangs r = d/2 die dazugehörige Kreisflächen-Formel A = π/4 * d2.
Online Kreis-Rechner – Kreisumfang + Kreisfläche berechnen
Dieser Kreisrechner basiert auf dem Rechner für Kreise von Arndt Brünner.
Creative Commons Attribution Non-commercial Share Alike License 4.0
So ein Kreis-Rechner ist auf jeden Fall bequemer zu handhaben als derlei Aufgaben zu Fuß berechnen zu müssen. Selbst mit dem Näherungswert 3.14 für Pi ist man ohne Taschenrechner schon ordentlich mit dem Rechnen beschäftigt.
Herleitung der Kreisflächen Formel
Kreisflächen berechnen können ist das eine, verstehen wie es zu der Formel kommt das andere. Man kann die Herleitung bzw den Beweis auf verschiedene Arten führen. Zum Beispiel über das Integral einer Kreisfunktion, über eine Intervallschachtelung mit Vielecken a la Archimedes oder am anschaulichsten über das Zerlegen des Kreises in Teilstücke, die man dann in eine rechteckige Form einzubetten versucht. Siehe u.a. bei den Mathematischen Basteleien.
Das folgende Youtube Video zeigt die Variante mit dem Zerlegen des Kreises in Teilstücke.
Wer spielerisch die Entstehung der Formel zur Kreisflächenberechnung erleben möchte, der kann das mit Hilfe der genialen Geometrie Software GeoGebra tun. Die folgende interaktive App zeigt, wie eine Kreisfläche in Kreissektoren zerlegt wird und die Einzelteile dann am Umfang abgewickelt und geschickt umarrangiert werden.
Ihr müsst einfach mal mit den drei horizontalen Reglern rumspielen. Dann seht ihr, wie sich der Kreis abwickelt, die Sektoren immer feiner werden und am Ende sich alles zu einer rechteckigen Fläche verzahnt – schöner kann man die Transformation von Kreisfläche zu Rechteck kaum darstellen.
Mit zunehmender Unterteilung passt sich die Fläche immer mehr der Fläche eines Rechtecks mit der Höhe des Kreisradius und der halben Länge des Kreisumfangs an. Bekanntlich ist die Formel für den Flächeninhalt eines Rechtecks Höhe mal Breite – hieraus ergibt sich dann für die assoziierte Kreisfläche r*π*r – und damit die gesuchte Kreisflächenformel.
Hinweis zu Bildrechten: Wikipedia (der GNU-Lizenz für freie Dokumentation) – Ein Kreis mit Mittelpunkt, Radius und Durchmesser – @ Sven