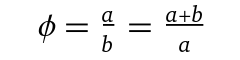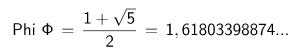Die Zahl Phi [ Φ ] ist eine eng mit Kunst und Schönheit verwobene irrationale Zahl. Ähnlich wie bei der Zahl Pi reicht die Geschichte der Zahl Phi bis weit in die Zeiten vor Christi Geburt zurück. Euklid soll sie als erstes definiert haben, damals noch unter der Bezeichnung „Goldene Zahl“ bzw. „Goldener Schnitt“. Heutzutage wird in der Regel das griechische Symbol Phi Φ verwendet, wenn es um den Wert des Goldenen Schnittes geht.
Definition des Goldenen Schnitts: Der Goldene Schnitt beschreibt ein Teilungsverhältnis, bei dem das Verhältnis des Ganzen zum größeren Teil dem Verhältnis des größeren zum kleineren Teil entspricht. Mathematisch ausgedrückt: a/b = (a+b)/a. Dieses Verhältnis ist Φ ≈ 1,618.
Durch geschickte Umstellung kann zur Berechnung von Phi die folgende Quadratische Gleichung gewonnen werden:
Aus dieser Quadratische Gleichung lässt sich die folgende positive Lösung ableiten:
Dieser Zahlenwert ist also der Kern des goldenen Schnittes. Wenn man den Kehrwert dieser Zahl bildet und mit dem originalen Wert vergleicht, dann erlebt man eine kleine Überraschung. Die Nachkommastellen der beiden Zahlen sind identisch. Und jetzt vergleicht diese beiden Zahlen bitte noch mal mit dem Quadrat von Phi. Das ist Überraschung Numero Zwo, Phi zum Quadrat liefert die selben Nachkomastellen wie Phi und der Kehrwert von Phi.
1/Φ = 0.618033988749…
Φ = 1.618033988749…
Φ2 = 2.618033988749…
Übrigens, da Phi die Nullstelle eines Polynoms darstellt, ist die Zahl nicht transzendent.
Der Goldene Schnitt in der Natur und Kunst
Der Goldene Schnitt findet sich erstaunlich oft in der Natur wieder, beispielsweise in der Anordnung von Blättern an Pflanzen, in der Struktur von Schneckenhäusern oder in der Verteilung von Sonnenblumenkernen. Auch in der Kunst und Architektur wurde der Goldene Schnitt seit der Antike bewusst eingesetzt, um harmonische Proportionen zu erzeugen (z.B. im Parthenon in Athen oder in Werken von Leonardo da Vinci).
Erstaunlich ist das Verhalten der Fibonacci-Zahlen: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
Das Bildungsgesetz dieser Zahlenreihe ist ganz einfach, das Folgeglied ist die Summe der beiden vorangegangen Elemente. 1+1=2, 1+2=3, 2+3=5, 3+5=8 usw.
Was hier überrascht ist das Verhalten zweier Folgewerte, wenn man sie dividiert.
Beispiel: 8/5 = 1.6 oder 55/34 = 1.6176.. oder 17711/10946 = 1.61803398502..
Wer aufgepasst hat wird erkennen, dass die Folge der Fibonnaci Ouotienten gegen Φ konvergiert.
Phi – Ein ganz besonderer Kettenbruch
Die Zahl φ (Phi) hat viele faszinierende Eigenschaften – eine davon ist ihre Darstellung als unendlicher Kettenbruch:
φ = 1 + 1 / (1 + 1 / (1 + 1 / (1 + …)))
Dieser Kettenbruch ist ein Beispiel für eine periodische Kettenbruchdarstellung – er wiederholt sich mit dem gleichen Muster. Solche Darstellungen sind typisch für quadratische Irrationalzahlen, also Wurzeln aus Zahlen, die keine ganzen Zahlen sind.
Beziehung zur Fibonacci-Folge
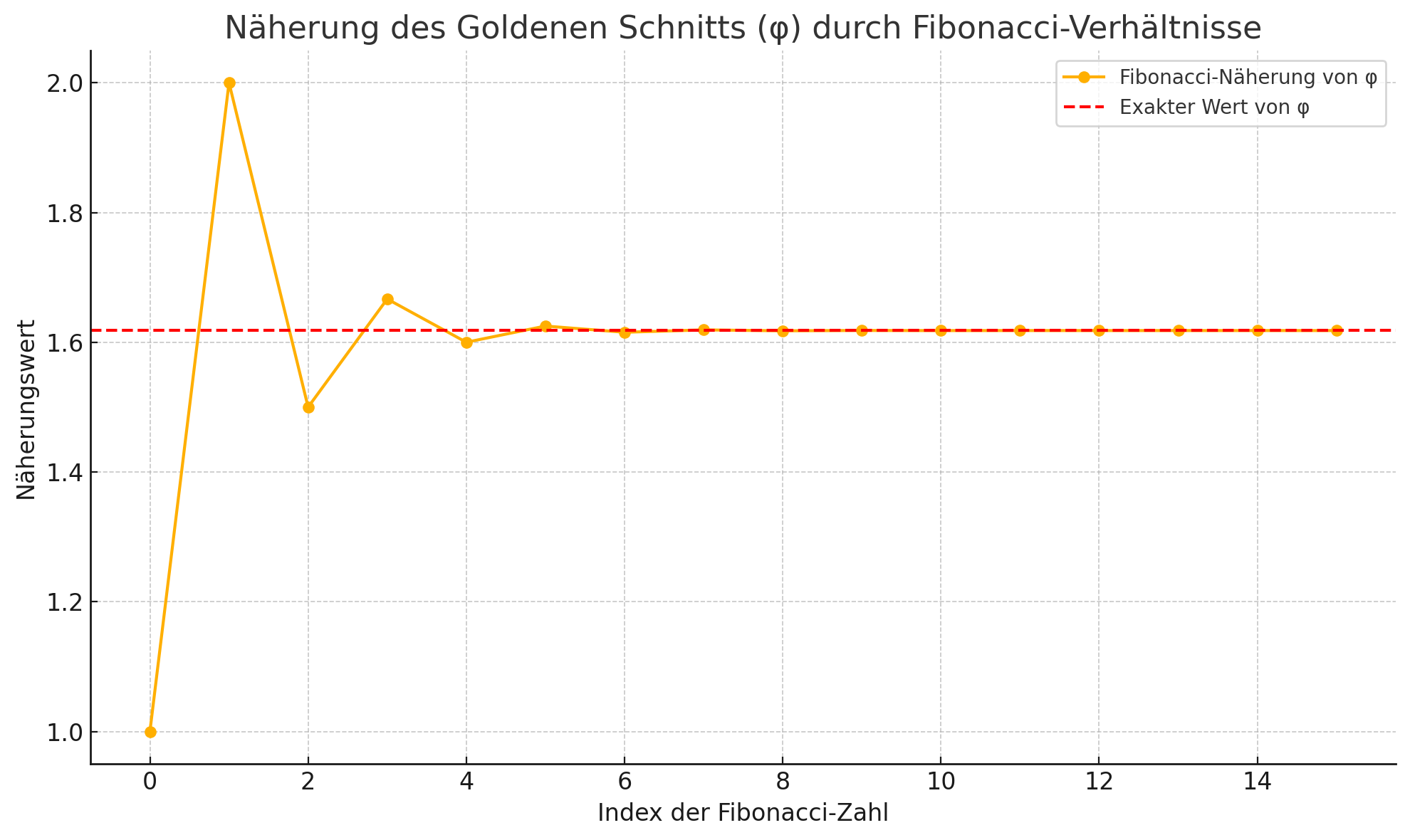
Ein interessantes Merkmal: Die Kettenbruch-Näherungen von φ sind eng mit der Fibonacci-Folge verbunden. Wenn man den Kettenbruch schrittweise abbricht (z.B. nach 1, 2, 3, … Schritten), erhält man Näherungswerte wie:
• 1/1 = 1
• 2/1 = 2
• 3/2 = 1.5
• 5/3 ≈ 1.666…
• 8/5 = 1.6
• 13/8 ≈ 1.625
• 21/13 ≈ 1.615…
Diese Brüche bestehen aus aufeinanderfolgenden Fibonacci-Zahlen. Der Grenzwert dieser Quotienten ist φ.
Einzigartigkeit
φ ist die am schlechtesten durch rationale Zahlen approximierbare irrationale Zahl. Das bedeutet: Unter allen irrationalen Zahlen ist sie eine derjenigen, die am wenigsten „rational aussieht“ – sie lässt sich sehr schlecht durch einen einfachen Bruch darstellen. Diese Eigenschaft macht sie in der Zahlentheorie besonders.
Die ersten 100 Nachkommastellen von Phi
φ=1.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911374…
Die Zahlen Phi und Pi werden auch schon mal gerne verwechselt, was sich in Analysen von Google Suchanfragen ablesen lässt.